「応用数学 - 特殊関数」の版間の差分
ナビゲーションに移動
検索に移動
図. 誤差関数のグラフ 図. ガンマ関数のグラフ 式 を使用すると、 の時でも を求めることができる。 図. 定義域を拡張したガンマ関数のグラフ 図. 単位階段関数のグラフ 図. : から別のグラフ のグラフになる関数
(→誤差関数) |
(→誤差関数) |
||
| 42行目: | 42行目: | ||
* 誤差関数は奇関数である。 | * 誤差関数は奇関数である。 | ||
* 測定値が正規分布になっていて、標準偏差が <math>\sigma</math> 、平均が <math>0</math> の場合、1つの測定値の誤差が <math>-a</math> と <math>a</math> の間になる確率は以下で与えられる。 | * 測定値が正規分布になっていて、標準偏差が <math>\sigma</math> 、平均が <math>0</math> の場合、1つの測定値の誤差が <math>-a</math> と <math>a</math> の間になる確率は以下で与えられる。 | ||
<br><br> | |||
== ガンマ関数 == | |||
定義: | |||
以下の無限積分で定義された関数 <math>\Gamma(p)</math> をガンマ関数(gamma function)という。 | |||
<math>\Gamma(p) = \int_{0}^{+ \infty} {x^{p - 1} \, e^{-x} \, dx} \qquad (p > 0)</math> | |||
<math>\Gamma(p)</math> を <math>p</math> の初等関数で表すことはできない。 | |||
<math>p</math> が正の整数の時や、分母が2である分数の時は簡単に値を求めることができる。 | |||
<br> | |||
[[ファイル:Special Function 2.png|フレームなし|中央]] | |||
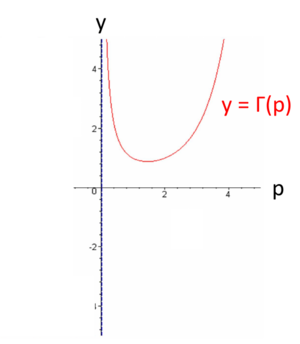
<center>図. ガンマ関数のグラフ</center><br> | |||
<br> | |||
ガンマ関数は、階乗の概念を一般化した特殊関数である。<br> | |||
互いに同値ないくつかの定義が存在する。<br> | |||
<br> | |||
1729年、オイラーにより階乗の概念の複素数への一般化として、最初に導入された。<br> | |||
<br> | |||
自然数 <math>n</math> に対して、 <math>\Gamma(n + 1) = n!</math> が成立する。<br> | |||
階乗(factorial) : <math>n! = n(n -1)(n - 2) \, ... \, 3 \cdot 2 \cdot 1 \qquad ( n : \mbox{ 正 の 整 数 } )</math><br> | |||
<br> | |||
* ガンマ関数の性質<br> | |||
** <math>\Gamma(p + 1) = p \Gamma(p) \qquad (p > 0)</math> | |||
**: <math>p = n - 1</math> とおけば、以下が成立する。 | |||
**: <math>\Gamma(n) = (n - 1) \Gamma(n - 1)</math> | |||
** <math>\Gamma(1) = 1</math> | |||
** <math>\Gamma(n) = (n - 1)! \qquad (n = 2, 3, 4, \cdots)</math> | |||
** <math>\Gamma \left( \frac{1}{2} \right) = \sqrt{\pi}</math> | |||
** <math>\Gamma \left( \frac{n}{2} \right) = \left( \frac{\sqrt{\pi}}{2^{m}} \right) \, (2m - 1) \,(2m - 3) \, \cdots 3 \cdot 1 \qquad (m, n : \mbox{ 正 整 数 }, \, n = 2m + 1 : \mbox{ 奇 数 } )</math> | |||
<br> | |||
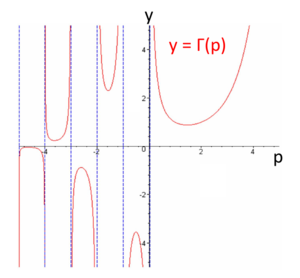
<center>式 <math>\Gamma(p + 1) = p \Gamma(p)</math> を使用すると、 <math>p < 0</math>の時でも <math>\Gamma(p)</math> を求めることができる。</center><br> | |||
[[ファイル:Special Function 3.png|フレームなし|中央]] | |||
<center>図. 定義域を拡張したガンマ関数のグラフ</center><br> | |||
<br> | |||
例題: | |||
以下のガンマ関数の値を求めよ。 | |||
(1) <math>\Gamma(3)</math> | |||
(2) <math>\Gamma \left( \frac{3}{2} \right)</math> | |||
解答: | |||
(1) <math>\Gamma(3) = (3 - 1)! = 2</math> | |||
(2) | |||
<math>\begin{align}\Gamma \left( \frac{3}{2} \right) &= \left( \frac{3}{2} - 1 \right) \, \Gamma \left( \frac{3}{2} - 1 \right) \\ &= \frac{1}{2} \, \Gamma \left( \frac{1}{2} \right) \\ &= \frac{\sqrt{\pi}}{2} \end{align}</math> | |||
<br><br> | |||
== 単位階段関数 == | |||
定義: | |||
以下で定義された関数U(t)を単位階段関数(unit step function)という。 | |||
<math> | |||
U(t) = | |||
\begin{cases} | |||
0 & \qquad (t < 0) \\ | |||
1 & \qquad (t \ge 0) | |||
\end{cases} | |||
</math> | |||
<br> | |||
単位階段関数は、ヘビサイドの階段関数(Heaviside step function)とも呼ばれる。<br> | |||
ただし、 <math>t = 0</math> の場合の扱いが異なるもの(例えば、 <math>t = 0</math> の値を未定義とする)をそう呼ぶ場合もある。<br> | |||
<center>図. 単位階段関数のグラフ</center><br> | |||
<br> | |||
単位階段関数 <math>U(t)</math> は、時刻 <math>t</math> の関数として用いられることが多い。<br> | |||
<math>t = 0</math> においてグラフを(別の)グラフ <math>f(t)</math> に変えたい時、積 <math>U(t)f(t)</math> を作れば、その関数を表現することができる。<br> | |||
<br> | |||
さらに、時刻 <math>t = a</math> において突然変化するような現象を表したいときは、 <math>U(t)f(t)</math> をt軸へa方向だけ移動して <math>U(t - a)f(t - a)</math> とすればよい。<br> | |||
<center>図. <math>U(t)f(t)</math> : <math>t = 0</math> から別のグラフ <math>f(t)</math> のグラフになる関数</center><br> | |||
<br> | |||
例題:<br> | |||
以下の関数のグラフを書け。<br> | |||
<math>y = U(t) \, \sin{t}</math><br> | |||
<br> | |||
解答:<br> | |||
<math>y = U(t) \, \sin{t}</math> のグラフは以下のようになる。<br> | |||
ある関数に単位階段関数 <math>U(t)</math> を乗算する <math>t < 0</math> の時、値が <math>0</math> になる。<br> | |||
<br><br> | <br><br> | ||
2023年9月4日 (月) 11:18時点における版
概要
- 誤差関数について理解する。
- ガンマ関数について理解する。
- 単位階段関数について理解する。
- デルタ関数について理解する。
- 双曲線関数について理解する。
特殊関数とは
特殊関数(special functions)とは、特定の分野で何らかの名前や記法が定着している関数のことを指す。
何が特殊関数であるかのはっきりした定義は存在しない。
しばしば特殊関数として扱われるものには、ガンマ関数、ベッセル関数、ゼータ関数等がある。
特殊関数という用語は、初等関数の対義語ではない。
ある関数が初等関数であって同時に特殊関数とされる場合もある。
- ラプラス変換で扱う特殊関数
- ラプラス変換では、以下のような特殊関数を扱う。
- 誤差関数(ガウスの誤差関数)
- ガンマ関数(オイラーのガンマ関数)
- 単位階段関数(ヘビサイドの単位階段関数)
- デルタ関数(ディラクの衝撃関数)
誤差関数
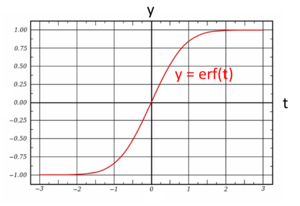
定義1: 以下の式で定義された関数erf(t)を誤差関数(error function)という。 定義2: 以下の式で定義された関数erfc(t)を相補誤差関数(complementary error function)という。
誤差関数は、ガウスの誤差関数(Gauss errorfunction)とも呼ばれる。
ガウスの誤差関数 :
誤差関数には、以下のような特徴がある。
- 誤差関数は奇関数である。
- 測定値が正規分布になっていて、標準偏差が 、平均が の場合、1つの測定値の誤差が と の間になる確率は以下で与えられる。
ガンマ関数
定義: 以下の無限積分で定義された関数 をガンマ関数(gamma function)という。 を の初等関数で表すことはできない。 が正の整数の時や、分母が2である分数の時は簡単に値を求めることができる。
ガンマ関数は、階乗の概念を一般化した特殊関数である。
互いに同値ないくつかの定義が存在する。
1729年、オイラーにより階乗の概念の複素数への一般化として、最初に導入された。
自然数 に対して、 が成立する。
階乗(factorial) :
- ガンマ関数の性質
-
- とおけば、以下が成立する。
-
例題: 以下のガンマ関数の値を求めよ。 (1) (2) 解答: (1) (2)
単位階段関数
定義:
以下で定義された関数U(t)を単位階段関数(unit step function)という。
単位階段関数は、ヘビサイドの階段関数(Heaviside step function)とも呼ばれる。
ただし、 の場合の扱いが異なるもの(例えば、 の値を未定義とする)をそう呼ぶ場合もある。
単位階段関数 は、時刻 の関数として用いられることが多い。
においてグラフを(別の)グラフ に変えたい時、積 を作れば、その関数を表現することができる。
さらに、時刻 において突然変化するような現象を表したいときは、 をt軸へa方向だけ移動して とすればよい。
例題:
以下の関数のグラフを書け。
解答:
のグラフは以下のようになる。
ある関数に単位階段関数 を乗算する の時、値が になる。